Fizika I.
Molnár
Péter, ELTE-SEK, molnarp65@gmail.com,
http://pmolnar.nhely.hu/
Mozgás, dinamika: derivált,
sebesség, gyorsulás, mértékegységek, SI egységrendszer, Newton
törvények, gravitációs törvény, egyenletesen gyorsuló mozgás
Scale of the universe
Számok mérnöki, tudományos írásmódja
Például:
- 25 000 = 2,5 · 104
- –80 = –8 · 101
- 0,009 = 9 · 10−3
Feladatok:
- egy proton tömege
0,0000000000000000000000000016726 kg, azaz 1,6726×10−27 kg,
és
- egy elektron tömege
0,00000000000000000000000000000091093822 kg, azaz 9,1093822×10−31 kg.
Hányszor nehezebb a proton az elektronnál?
Hány bacilus férhet egy pohár vízbe?
Mennyi idő alatt sétálná körbe egy hangya a földet? És egy csiga?
Találjunk ki feladatokat...
https://rexades.web.elte.hu/diakjaimnak/mereselmelet.pdf
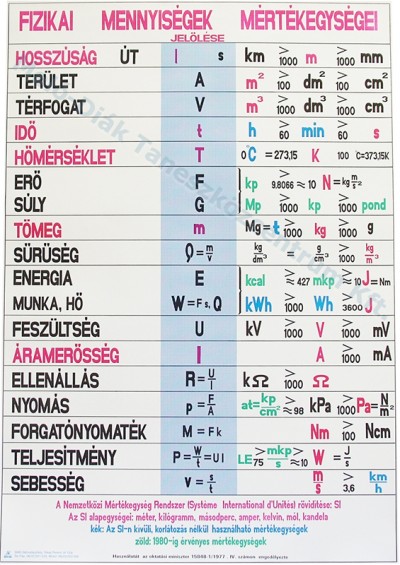
Származtatott mértékegységek: lásd könyv, valamint a mérési standardok
definíciója és története is ott található.
Koordináta rendszerek:
A koordináta-rendszer egy tér (vagy sík, egyenes, görbe,
felület stb.) pontjait bizonyos
alapelemekhez
(bázisokhoz) viszonyítva egyértelműen meghatározó
rendszer. Egy pont helyzetét a koordináta-rendszerben számokkal
(koordinátákkal) adhatjuk meg. A koordináta-rendszereket feloszthatjuk
dimenziószámuk (1, 2, 3, …, n dimenziós)
és a méretek jellege szerint:
- Affin (pl. Descartes-féle, carthesianus):
a koordináták hosszúságok (távolságok) mérőszámai
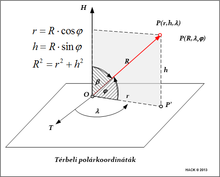
- Poláris: a koordináták hosszúságok és
szögek mérőszámai
- Görbe vonalú (pl. elliptikus,
geodetikus): a koordináták egy önkényesen felvett hálózat skálázásából
adódnak
- Homogén (pl. baricentikus, projektív): a
koordináták nem abszolút méretek, hanem viszonyszámok (méretarányok)
- Egyéb, főként felületek pontjainak
megadására szolgáló (pl. földrajzi és csillagászati
koordináták
KÖNYV: koordináta rendszerek pg. 19.
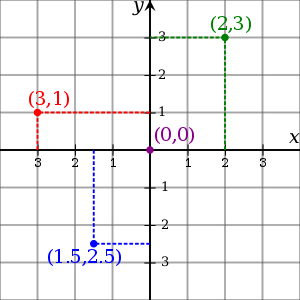
Descartes-féle derékszögű koordinátarendszer
Nevezetes ponthalmazok: https://matekarcok.hu/nevezetes-ponthalmazok-mertani-helyek/
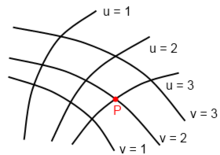
Görbe vonalú koordinátarendszer
Koordináta
gyakorlatok
Polár koordináták: https://www.youtube.com/watch?v=TL5FAGO90bU
Gyorsuló, forgó koordináta rendszerek: http://theorphys.elte.hu/~drotos/Faem/Gyorsulo.pdf
http://www.mozaweb.hu/Lecke-FIZ-Fizika_9-9_Tehetetlensegi_erok_Kiegeszito_anyag-100012
The
effective acceleration of gravity at the poles is
980.665 cm/sec/sec while at theequator it
is 3.39 cm/sec/sec less due to the centrifugal force. If you weighed 100
pounds at the north
pole on
a spring scale, at the equator you
would weigh 99.65
pounds, or 5.5 ounces less.
A mozgások leírása, az ehhez szükséges
mennyiségek, jellemzők ismerete, használatuk begyakorlása.
Vektorok
Deriválás
Integrálás
Kinematika --- mozgások klasszikus leírása
Kinematika
sulinet
Kinematika
részletesebb
Dinamika:
mozgástörvények, erőhatások, a mozgás oka


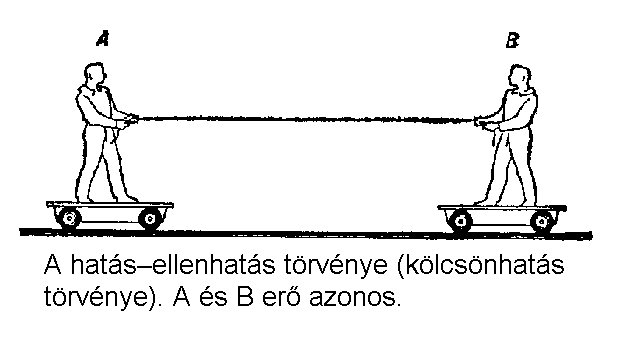
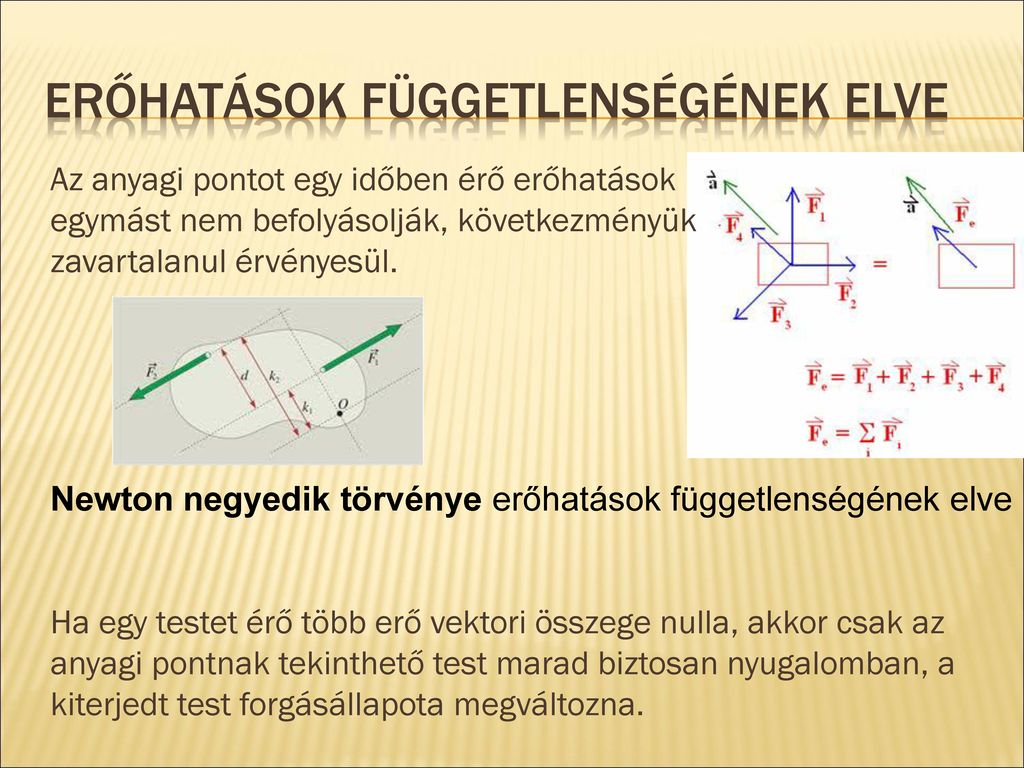

Impulzusmegmaradás ---- Newton II. törvénye
---- Impulzusmomentum megmaradása ---- Energiamegmaradás
Mozgással
kapcsolatos feladatok 1.
Feladatok
eredeti
Egyenesvonalú
gyorsuló mozgás
Mozgas
feladat nehézségi erő, surlódás
Körmozgás
 Néhány
feladat az előadás közepén. Ugyanitt rezgő mozgás és feladatok
Néhány
feladat az előadás közepén. Ugyanitt rezgő mozgás és feladatok
Rezgőmozgás
Hullámmozgás
Káosz, fraktálok
Fraktálok,
káosz
Video Oszcilláló
reakciók











 Néhány
feladat az előadás közepén. Ugyanitt rezgő mozgás és feladatok
Néhány
feladat az előadás közepén. Ugyanitt rezgő mozgás és feladatok