Bb5t2501 Biostatisztika GY
Tematika
Előadó:
Molnár Péter docens, ELTE-SEK
állattan C. épület 326. molnarp65@gmail.com 30/8975550 http://pmolnar.nhely.hu/
Tantárgyfelelős: Podani János § Pásztor Erzsébet
tanszékvezető
egyetemi tanár § adjunktus XF4SL5 § LVYMSR
Tematika
Biostatisztika Tematika 2022
- A véletlen fogalma.
Köznyelvi és matematikai értelmezés. Véletlen folyamatok. Biológiai
véletlen tömegjelenségek.
Készségfejlesztés: grafikonok értelmezése (folyamatos)
- Relatív gyakoriság, várható
érték és valószínűség
Készségfejlesztés: adatrögzítés, iteratív kalkuláció,
grafikonok készítése táblázatkezelő alkalmazással, csoportmunka google
eszközök igénybe vételével (folyamatos) genetikai jelenségek
valószínűségét meghatározó mechanizmusok 1. Egy lokusz, meiózis
- Feltételes relatív
gyakoriság, feltételes valószínűség és függetlenség. Szórás. Készségfejlesztés:
eloszlások ábrázolása, táblázatos statisztikai eredmények értelmezése,
szakcikk olvasás, becslés
- A binomiális eloszlás Készségfejlesztés:
matematikai modell és véletlen biológiai tömegjelenségek összekapcsolása
a véletlen kísérlet fogalmán keresztül, több lépésből álló kalkulációk
táblázatkezelő alkalmazásban, empírikus adatok értelmezése modellek
alapján,
- Gyakorlás, összefoglalás
- Számonkérés
- Diszkrét eloszlások. Leíró
statisztikák.,
Készségfejlesztés:
szisztematikus keresés a neten, a keresés eredményének dokumentálása,
szakcikk olvasás, grafikonok, statisztikai eredmények értelmezése, a
tanultak alkalmazása publikációk megértésére, saját bibliográfia
felállítása
Szünet - feladat:
- Biológiai jelenségeket
magyarázó eloszlások Geometriai, Polinomiális, Poisson és normális
eloszlású biológiai változók kapcsolata a binomiálissal. Készségfejlesztés: modell-jelenség összekapcsolás képességének fejlesztése
- Hipotézis vizsgálat 1.
Előjelteszt
Készségfejlesztés: empírikus adatok értelmezése modellek
alapján, angol szakcikkolvasás
- Hipotézis vizsgálat: 2.
Illeszkedés vizsgálat
Készségfejlesztés: empírikus adatok értelmezése modellek
alapján
- Számonkérés
- A számítógépes szimulációs
modellezés eljárásának megértése egy konkrét példán .
- . Statisztikai eredmények
értelmezése.
Készségfejlesztés:
Irodalmazás, saját bibliográfia felállítása
Javító ZH a félév anyagából
Követelmények és értékelés
A gyakorlati munka előkészítő, a
gyakorlaton elvégzendő és házi feladatokból áll. Ezek értékelése bináris,
elfogadott. illetve nem elfogadott. Elfogadott az a feladat, aminek a
teljesítési minősége legalább elégséges. Gyakorlati jegy szerzésének
feltétele a feladatok 80%-át elfogadottra teljesíteni, összhangban azzal,
hogy maximum 3 gyakorlatról lehet hiányozni. Az érdemjegy kettő illetve három részből áll. Alapesetben két, a
gyakorlatok idéjére időzített összefoglaló feladatsor önálló elvégzésére
kapott jegyből. Ezt javíthatja a magasszínvonalú gyakorlati munka
elismeréséül kapott jeles érdemjegy. Akinek valamelyik részjegye
elégtelen, az a félév végén javító ZH-t írhat, a teljes félév anyagából.
Akinek az elfogadott feladatai nem érik el a kiadott feladatok 80%-át, az
a gyakorlat megismétlésére kényszerül.
Kommunikációs eszközök
Az egyes gyakorlatok feladat lapokra
épülnek, amiket a gyakorlatok elején kiosztok és ebbe a dokumentumba is
bemásolok. Adatokat google táblázatok formájában oszthatunk meg egymással.
A gyakorlaton elvégzett és a házi feladatok benyújtása on-line történik.
Az első gyakorlat előtt mindenki hozzon létre egy x.y.biostat2022 nevű
google dokumentumot (x.y = a tulajdonos neve), ami az összes elvégzett
feladatot tartalmazza illetve dokumentálja. Ezt szerkesztésre ossza meg a
molnarp65@gmail.com címmel. A feladatok saját számítógépen, Excell táblázatkezelővel
is elvégezhetőek, de a dokumentáció ugyanígy történik. A heti feladatok
megoldásait a gyakorlatot követő 5. nap 24h-ig kell a dokumentumban
rögzíteni. Legfeljebb kétszer kérhető 5 napos hosszabbítás, amit a
csoportok számára létrehozandó google naptárban kell megtenni.
A gyakorlaton feldolgozott
tananyag
RHS Biostatisztika könyv -az R
program használatára vonatkozó példák kihagyandóak
Reiczigel
Jenő, Harnos Andrea, Solymosi Norbert 2007: Biostatisztika nem
statisztikusoknak Pars. 455. Oldal
Feladatgyüjtemény
(
Zemankovicsné
dr. Hunkár Márta, Pannon Egyetem)
Használható
jegyzet: Szörényi, Széchenyi Egyetem Fejezetek 1-7-ig
Szükséges előismeretek: 6-8
Bevezetés: Miért tanuljunk
statisztikát 13-22 Elérhető: Bevezetés
Statisztikai alapfogalmak: 23-50
Események, valószínúség 3.1.
Fejezet 51-56
Valószínúségi változók 3.4.
Fejezet 60-68
Valószínúségszámítás és
statisztika kapcsolata 82-85
Leíró statisztika 87-118
Becslés 123-29, 131-38,
5.3.1-5.3.2, 139-41, mintaelemszám meghatározása 5.7.példa, 148.oldal
Hipotézis vizsgálat 151-63, 164-82
Előjel próba 227-28
Eloszlásokra vonatkozó próbák: Illeszkedés vizsgálat, 206-9,
Függetlenség vizsgálat 212-16, homogenitás vizsgálat 218-19,
Várható értékekre vonatkozó
próbák: Egy
mintás z-próba 194-5, Egy mintás t-próba 195, ,
Csak könyvből:
kétmintás z-próba, t-próba 196-7
Varianciákra vonatkozó próba: F-próba 203
Korreláció számítás 241-45
Regresszió számítás 251-253
Korábbi
előadás anyagai (COVID miatt videóval is)
Kereshető/letölthető
valós feladatok/adatok
Chi2
genetika példa
https://archive.ics.uci.edu/ml/datasets.php
https://college.cengage.com/mathematics/brase/understandable_statistics/7e/students/datasets/svls/frames/frame.html
https://www.zoology.ubc.ca/~whitlock/ABD/teaching/datasets/02/datasets02.html
https://www.ksh.hu/stadat
Bevezetés: Miért tanuljunk statisztikát 13-22
Statisztika nélkül nincs
kísérletes tudomány !!!!
Tudomány: ami
működik,
vagyis jóslásokra alkalmas. Ha igaz a hipotézis, akkor annak minden
következménye igaz (összhangban áll a valósággal)
- mérésének szerepe
http://www.szabadgondolkodo.hu/ismeretterjesztes/tudomanyos-modszer.php
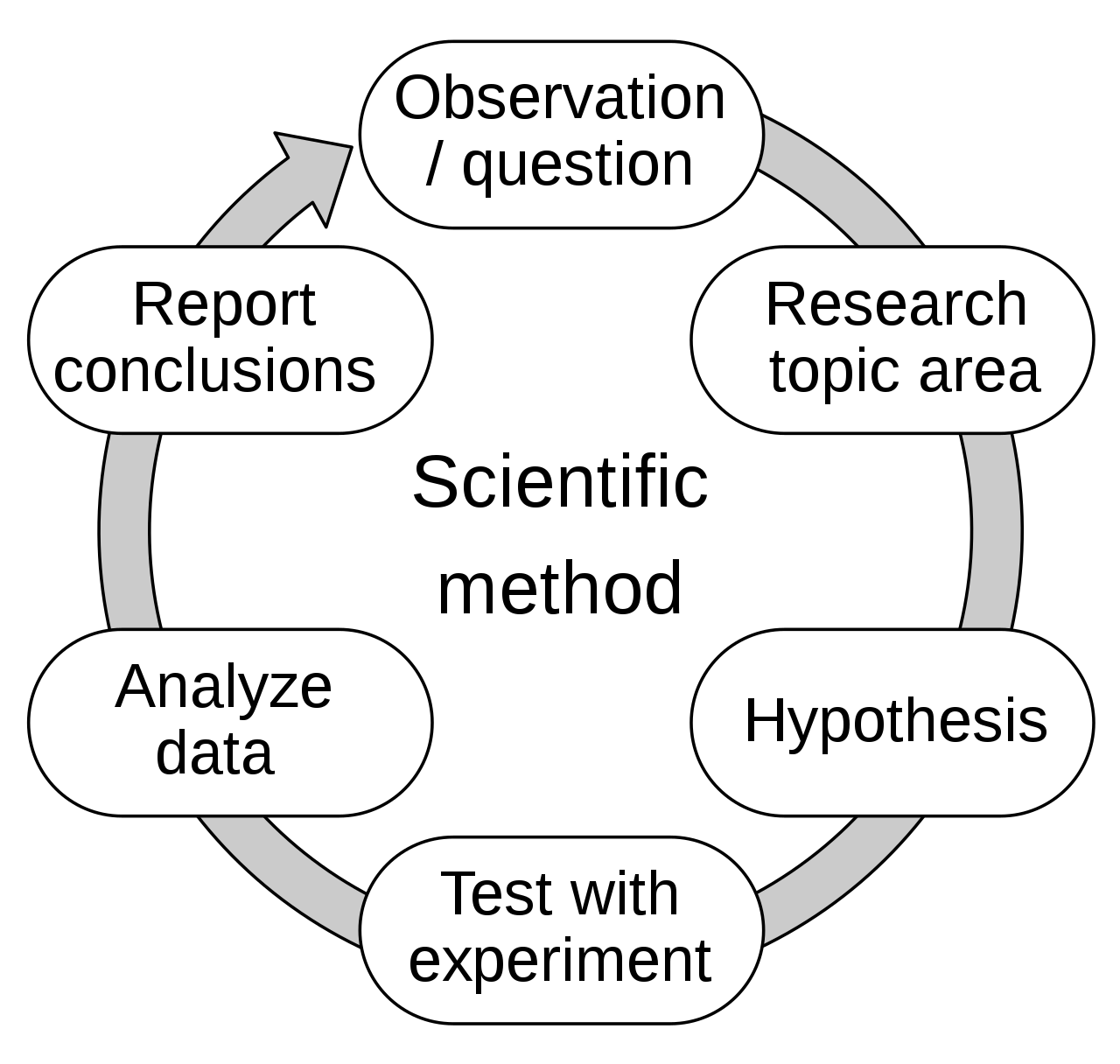
https://hmn.wiki/hu/Scientific_research
Hogyan döntjük el, hogy igaz-e a hipotézis? Hogyan
döntjük el, hogy egy mérés eredménye összhangban van-e a valósággal?
SOHA nem kapunk pontos eredményt, minden mérésben van hiba. Miért
nem pontosan azt kaptuk, mint amit vártunk? Csak zaj, vagy
szisztematikus hiba (rossz a hipotézis???)---→ Csak
valószínűségekről tudunk beszélni. A mérés eredménye nagy
valószínűséggel összhangban van a valósággal (jobban mondva a
tévedés esélye kicsi). STATISZTIKA!!!!
Mitől lesz tudományos egy mérés? Követelmény: meg kell
adni a cikkekben, hogy mekkora a tévedés esélye. Ha
közlünk egy eredményt, akkor azt is közölnünk kell, hogy ha valaki
elvégzi a mérést, akkor milyen eséllyel milyen eredményt kap. Vagyis
ha valaki tényleg ellenőriz bennünket (elvégzi a mérést) és kap
valami eredményt, akkor meg tudja mondani, hogy igazat mondtunk-e.
Minden tudományos eredmény NEM érték, hanem a lehetséges értékek
valószínűségi eloszlása. Pld: 3
± 0.25. Feltételezés: A
változó NORMÁL eloszlású.
Állításainkkal együtt azt is
közölni kell, hogy mi az esélye annak, hogy tévedünk. (Hipotézis tesztelés, 5%
szignifikancia szint –-→ 5% -nál kisebb annak a valószínűsége,
hogy hazudunk.) Politikusok?
A valóság tele van statisztikai
ábrákkal, tudnunk kell értelmezni őket.
Igazán nagyot hazudni/tévedni csak statisztikával lehet… Átlagfizetés emelkedése,
munkanélküliség,
http://www.szabadgondolkodo.hu/ismeretterjesztes/tudomanyos-modszer.php
Kitérő: adatbányászat, irodalomkutatás, adatfeldolgozás,
riport/előadás/szakdolgozat készítés
Mitől tudományos egy cikk? És mitől nem? Mi az a peer review process?
Referenciák, citációk szerepe.
Wikipédia
Web of Science
PubMed
Google scholar
Keresés kulcsszavak szerint, keresés linkek, referenciák alapján, alap
cikkek alapján
Információ feldolgozás --→ A vázlat nagyon fontos, mindíg tervezzünk előre,
de a tervet interaktív módon mindíg lehet módosítani az adatok függvényében.
Kísérlet tervezés rendkívül fontos, csak jól megtervezett kísérletet lehet
kiértékelni, ha utólag gondolkodunk, akkor szenvedünk.
Referencia manager: Mendeley
Word, Open Office, Excel, Calc, Gnumeric használlata.
Online kollaborációs eszközök használata google docs, google drive, dropbox
Grafikus eszközök : gimp
Prezi
Kísérletes kutatási
beszámoló szerkezete:
Miért
Mit
Hogyan
Mi az eredmény
Ez mit jelent
Hogyan csináljunk
tudományos cikket/beszámolót/előadást?
Adatok-→cím--→bevezetés-→eredmények-->megvitatás
A statisztika alapjai
A statisztika feladatai:
-
Adatok értelmezése,
ábrázolása, kiugró értékek kezelése
-
Valószínűség hozzárendelése
lehetséges kimenetelekhez
-
Állítások valóságtartalmának a
vizsgálata/hipotézis tesztelés
-
Változók kapcsolatainak a
vizsgálata
-
Kísérlettervezés
Tipikus kérdések és válaszok:
Mennyi? --- Lehetséges értékek valószínűség eloszlása --- átlag,
szórás (normál eloszlás) --- medián, percentilisek (nem normál eloszlás)
Igaz-e? --- Hipotézis tesztelés (átlagra, mediánra)
Van-e összefüggés? --- korreláció, regresszió
Egyváltozós – többváltozós
statisztika
Statisztikai
alapfogalmak: 23-50
Események, valószínúség 3.1. Fejezet
51-56
Valószínúségi változók 3.4. Fejezet
60-68
Alapok - definíciók
A leíró
statisztika (descriptive statistics) a statisztikának az az
ága, amelyik az adatokban rejlő információ emészthető formában való
tálalásával foglalkozik. Ez jelentheti az adatok rendezését,
csoportosítását (táblázatok), megjelenítését (grafikonok, diagramok,
piktogramok), illetve statisztikai mérőszámokkal való jellemzését
(minimum, maximum, átlag, szórás stb).
Az induktív
statisztika két legjellemzőbb feladata a becslés (estimation)
és a hipotézisvizsgálat (hypothesis testing). A becslés a ,,Mennyi?
Mekkora? Hány százalék? stb.’’ kérdésekre vár választ, mégpedig egy
(vagy néhány) számot. A hipotézisvizsgálatban ezzel szemben ,,Igen/Nem’’
választ várunk az ,,Igaz-e? Fennáll-e? Van-e összefüggés …? Van-e hatása
…? Van-e különbség …? stb.’’ kérdésekre.
Kétféle felfogás: Kísérletet végzünk, ennek lehetnek lehetséges
kimenetelei, amikor elvégezzük a kísérletet, ezek közül egy megvalósul. Ez
egy elemi esemény (véletlen
által meghatározott) kimenetele.
Másik felfogás szerint van egy (véges vagy végtelen) populáció, ebből
veszünk egy (véletlenül kiválasztott) mintát. Megállapítjuk a minta egy
tulajdonságát. Ezt a két szemléletmódot összevonjuk. Elemi eseményekről
beszélünk, ezeknek vannak lehetséges kimenetelei, amiből egy konkrét
értéket mérünk. A kimenetelek (valószínűségi változók) lehetséges típusai
(mérési skála) lehetnek: nominális, ordinális (kvalitatív), intervallum és
arányos (kvantitatív). Megkülönböztetünk még diszkrét és folytonos
változókat.
(olvasd el: mintavétel, visszatevéses, visszatevés nélküli mintavétel,
reprezentatív minta)
Valószínűség mérése/becslése (mindíg
lehetséges!):
Többször ismételt mérés --> A lehetséges kimenetelekből mindíg
realizálódik egy --> Gyakoriság hisztogram készítése --> Relatív
gyakoriság hisztogram (gyakoriság/mérések száma) --> Relatív gyakoriság
tart a kimenetel valószínűségéhez, ha a mérések száma tart végtelenhez.
Gyakoriság hisztogram folytonos változók esetén: csak az érték egy adott
intervallumba esésének mérésének van értelme. Véges populációk esetén a
teljes populáció megmérése adja a valószínűséget.
Másik módszer: Valószínűség számítható megfelelő matematikai modell
alapján. Egyenlő valószínűségű események, binomiális, poisson, normális
eloszlás. t-eloszlás, khi-négyzet eloszlás, F eloszlás.
Adatok ábrázolása
Grafikon
típusok
NAT1
NAT2
NAT3
Adatok önálló feldolgozása
Feladat
Kombinatorika
Gyakorlatok 2.
Sürüségfüggvény, eloszlásfüggvény
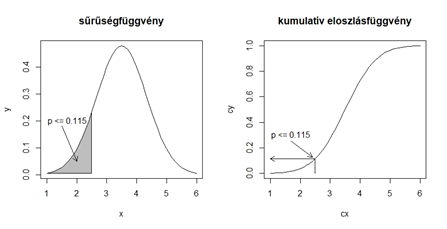
https://statisztikaegyszeruen.blog.hu/2019/03/08/a_valoszinusegi_eloszlasokrol_iii
Nevezetes eloszlások (Binomiális, Hipergeometrikus, Poisson
, Egyenletes, Exponenciális, Normális, Standard normális, t, khi
négyzet)
a Feladatgyüjteményből.
Az sürüségfüggvény illesztése: Maximum
likelihood módszer.
Feladatmegoldások (valószínűség
kiszámítása) EXCEL függvények segítségével a feladatgyüjteményből,
vagy
4 5.
Populációs paraméterek becslése mintákból. Pontbecslés, intervallum
becslés - konfidencia intervallum. Feladatok.


HA
események
bekövetkezésének valószínűségét tudjuk becsülni, akkor állítások
igazságtartalmát is meg tudjuk állapítani, ez a hipotézis
tesztelés. Próbastatisztika!!!
Könyvből vagy http://pmolnar.nhely.hu/Biostat/3_Hipotezis_teszteles.ppt
Hipotézis: Populációs paraméterekre (átlag, medián, esetleg szórás)
vonatkozó állítás. Általában egyenlőtlenséget tartalmaz.
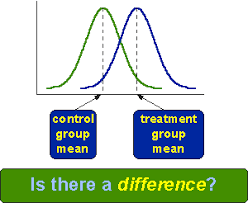

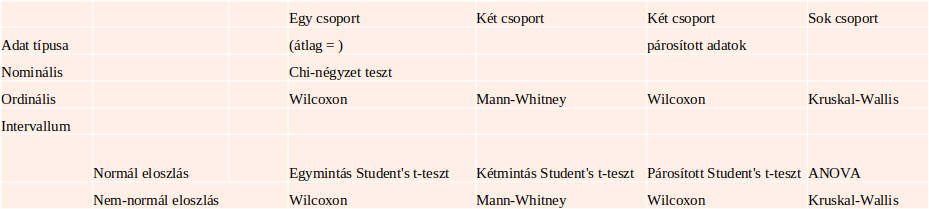
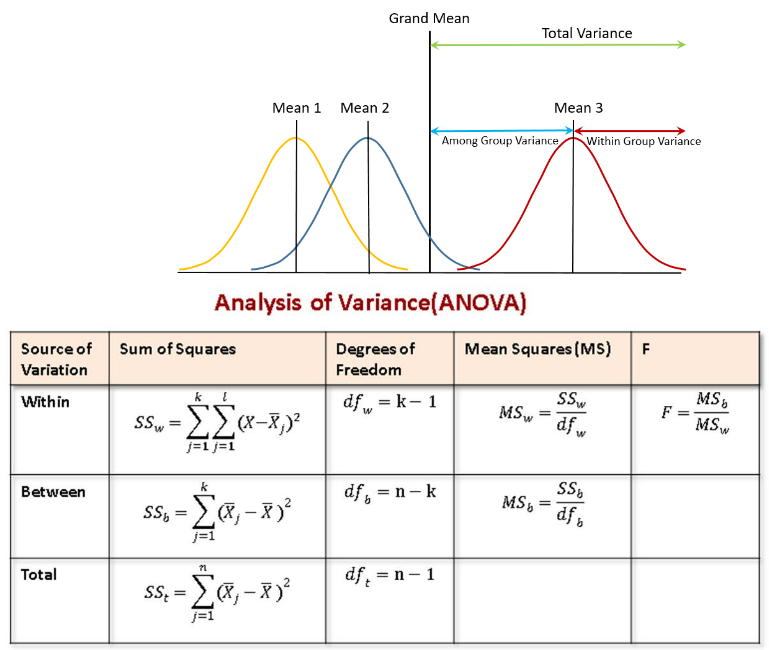
Khi2
teszt Függetlenség vizsgálat, modell jóságának
tesztje
Khi2 genetika példa
Összefüggésvizsgálat: Korreláció, regresszió








